Gauss distribution of bolt strength example

St. Paul's Statistics Introduction: Chapter 3

Computing Answers with the Binomial Equation

Section Goals:

Develop capability to build 'Pascal's Triangle'
Understand how to write the Binomial Distribution as an equation
Use terms from the Binomial Equation to solve real world problems
Build a Binomial PDF graph from the Binomial Equation

Binomial Distribution Use Criteria
the Binomial Distribution can be used when all 4 conditions below are met:

Results of each trial (coin flips, shell hits, failed students etc.) are independent. (i.e. if four coins are flipped, a coin landing 'heads' has no effect on the behaviour of its neighbours)
The probability of 'success' is known. (for a coin flip, it would be 50%)
The total number of trials (e.g. the number of coins pitched in the air) is known.
The total number of trials (e.g. the number of coins, cannon shells, students etc.) is less than 13.

When these four conditions are met, use of a Binomial Distribution is appropriate.

The method of solving real world problems using the Binomial Distribution will be taught by working an example. Commentary will be provided to explain different aspects of the example.

Example Problem Statement: Four coins are thrown in the air, and land as they choose. Develop a Binomial Equation that represents each term of the PDF.

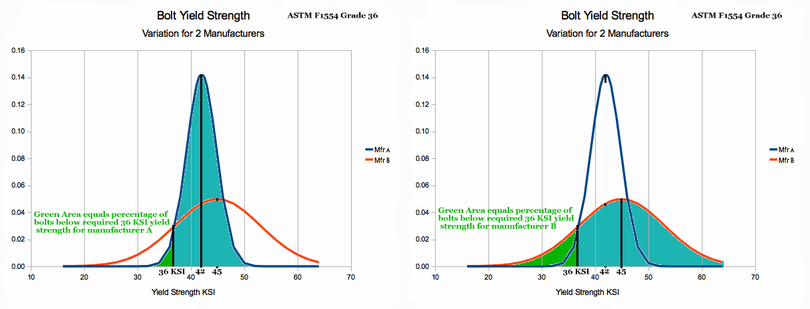
Step 1: Build Pascal's Triangle with a row that has one more number, than the problem has sample items or trials (be they coins, cannon shells or kittens). Pascal's Triangle will be used to provide numbers used in the probability formulas (4 coins->5 numbers)

Pascal's Triangle for writing Binomial Equations

Ch 3 Figure 1
The Steps for creating Pascal's Triangle are almost intuitive. Simply:

Write down the three 1's at the top of the triangle
Every place you find a pair of numbers side by side, total them & write the answers in the row below
Add 1's on the outside to enable creating another row. Apply Step 2 again until your triangle has enough numbers to meet the need of your number of trials. (How Many? If the number of coins, shells or whatever is n, then n+1 numbers are needed.)

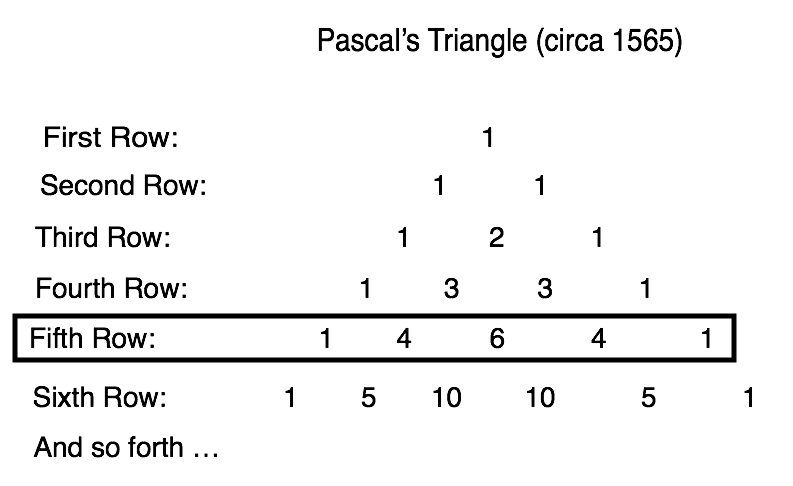
Step 2: p stands for success (e.g. heads up). q stands for failure (i.e. not heads up). Write pq pairs across the page until you have one more pq pair than there are samples in the problem (n=4 coins means you need 5 pq pairs).
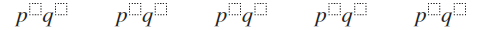
Writing a binomial equation step 2

Ch 3 Figure 2

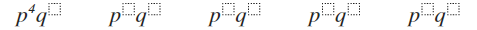
Step 3: Use the number of coins (4 in our example) as an exponent on the first p. Writing a binomial equation step 3

Ch 3 Figure 3

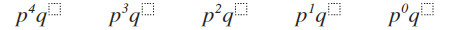
Step 4: Decrease the exponent by one each time you put it on the next pair. Continue until you have a zero exponent on the last p. (see below) Writing a binomial equation step 4

Ch 3 Figure 5

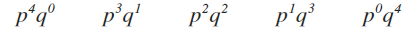
Step 6: Do the same thing for q, but work from right to left. Writing a binomial equation step 5

Ch 3 Figure 5

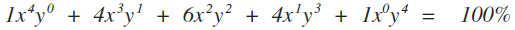
Step 6: Put 'plus' signs between all the terms and set the entire thing equal to 100% Writing a binomial equation step 6

Ch 3 Figure 6

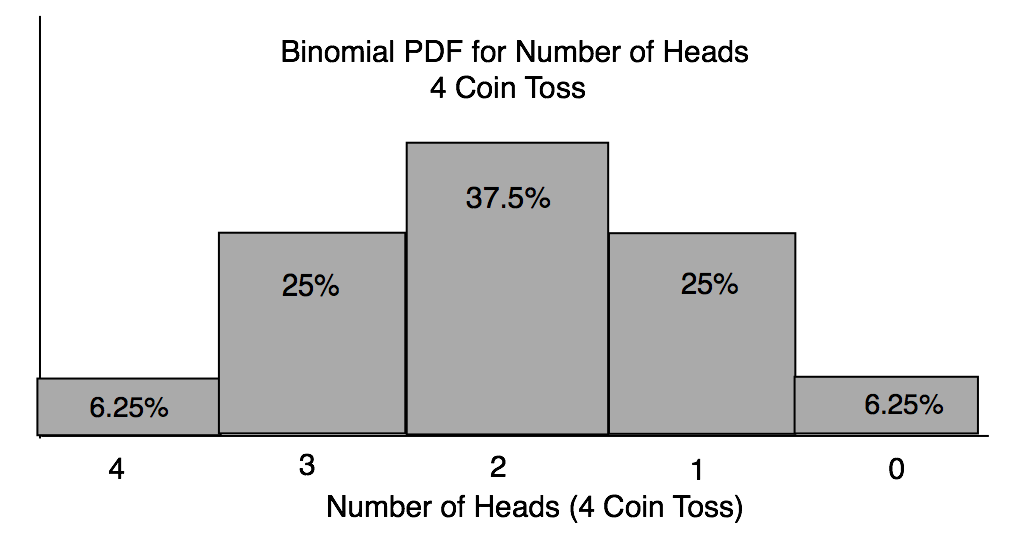
The equation you just wrote, is a math representation of the the following BINOMIAL PDF. We discuss that next. Graphic Probabilities for Binomial representing 4 coin tosses

Graphic Probabilities for Binomial representing 4 coin tosses

Ch 3 Figure 7
Discussion: The Binomial PDF has now been reduced to an equation, in which each of the terms represents the probability of one possible state (i.e. one of the bars in the PDF). Because this is true, we should be able to match each term (pq pair) to one of the bars on the PDF Ch 3 Figure 7.

You will need a scientific calculator with a y^x function button on it. Any calculator will do, but that y^x button makes the computations easier and reduces errors.

Ch 3 Figure 7 above is the PDF for the example problem being worked. Let us verify the second probability bar (i.e. probability of 3 heads). You will notice, that for 3 heads calculation, I choose the term with p^3. (i.e. p raised to power of 3). If I wanted the probability of 2 heads, I would compute based on the term with p^2.

P(3 heads) = 4* p^3 * q^1 = 4 * (.5^3) * (.5^1) = .2500 = 25.00%

The math confirms the the area of the bar for 3 heads.

For the example just worked, we now have a PDF Graph, and we have an equivalent PDF equation. While the method is a bit different from how it is done with the Gaussian Distribution, this should clarify how a PDF can be either in the form of an equation, or an equivalent graph. If both are done correctly, they 'say' the same thing. But for calculations, you will need the equation form. If you want to make sense out of it by looking, the PDF graph is far better. As said previously, the PDF graph is a road map to understanding the math.

Homework: Ch 3, Problem 1: Use the method above to compute the probability for each of the 5 possible outcomes of a 4 coin throw. (We just did the 2nd bar for you. Do the math for the other 4 bars). E-mail your answers to your teacher.

Homework: Ch 3 Problem 2:
Cats and Kittens:A veterinarian researcher has been keeping records for years on the color of kittens born in his office. He wants to know if color of the kitten matches a random variable, or if some other factor is at work in determining the color. His goal is to compare the probability to the office records.

A mother cat has 4 kittens. If the probability of a kitten being born black is 25%, what is the probability she will have exactly 3 black kittens?

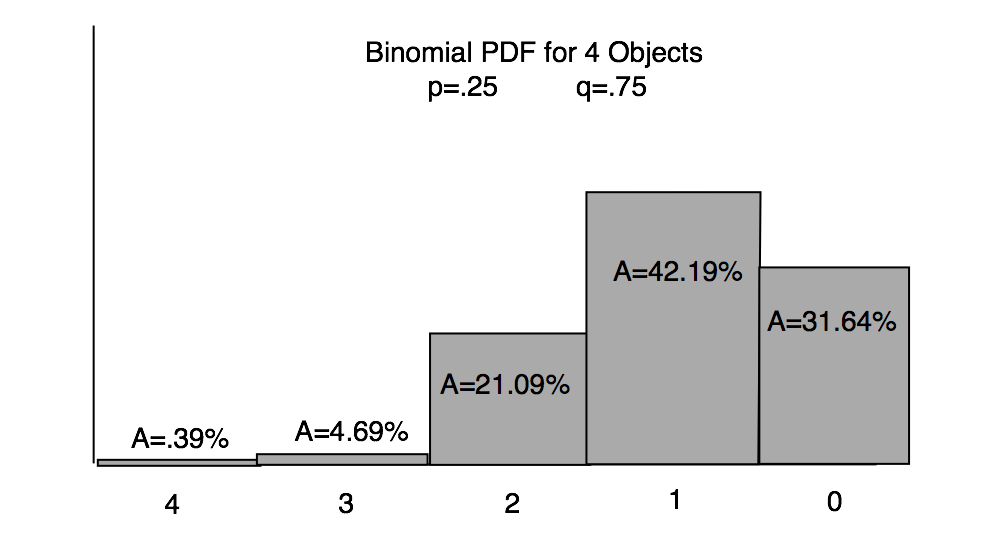
Graphic of Binomial Probabilities for black kittens (notional data)

Ch 3 Figure 8

First, check the problem to verify that a Binomial Analysis is appropriate. The Binomial criteria is provided at the beginning of this chapter. Do you think we can use the Binomial Equation? Do all four criteria see to be met?
Create the Pascal's triangle with a sufficient number of terms for this problem.
Create the Binomial Equation (all 5 terms) that describes the problem.
Choose the correct term. Fill in the probabilities and calculate the answer.
What is the answer? What is the probability of getting exactly 3 black kittens?
Does your answer agree with the PDF Ch 3 Figure 8?
E-mail your steps and the answer to your instructor.

Homework: Ch 3 Problem 3: The PDF for the coins is symmetric, but the PDF for the kittens is skewed to the right. What is unique about the problem statement that is causing one PDF to be symmetric and another to be skewed? E-mail your answer to your instructor.

Homework: Ch 3 Problem 4: Repeat Ch 3 Problem 1, but this time, assume a 'not black kitten' is success. Compute the probability of getting 0 or 1 or 2 or 4 'not black' kittens (refer to Probability Law 2). Should this answer be the same as what you got before? How can you use this observation to simplify problem solving? E-mail your answers to your instructor.

Homework: Ch 3 Problem 5:

For any problem in general, if the probability of success is 1%, what is the probability of failure?
Write the PDF equation for 6 bolts. Each bolt has a 1% chance of failure. Do not bother solving probabilities, just write the equation.
E-mail your answers to your instructor.

Beginning of St. Paul's Statistics Introduction

Dionysus.biz Home Page